Soft matter is a subdomain of physics concerned with flowing, deformable matter that is (mostly) of the mescoscopic scale. Materials under consideration are often subject to thermal flucuations, and entropy is a dominating factor in their dynamics / phase. Some examples: glasses, polymers, colloids, gels. Advances in Soft Matter have bearing on the plastics industry, the medical industry (models of cell membranes, organelles, on creation of synthetic biomaterials), on the development of 3D printing, and on the creation/advent of exotic materials.
Predominantly I work on liquid crystal theory and simulations. A liquid crystal is a state of matter wherein the constituent particles have orientational order, but lack positional order (as found in a traditional crystalline structure). I am interested in the dynamics and emergent behavior of dense suspensions of rod-like particles - in the dense regime, rods enter an ordered phase where they align with each other (driven by entropy), and this is a liquid crystal. In particular, I have investigated the effect of frictional interactions between rigid rods under shear.
- How does friction affect the steady state order of rods?
- Can the torque from low shear rates "balance" with frictional torques to maintain and isotropic state?
- Can one use a dissipation minimization argument to derive a theoretical framework for fricitonal rods?
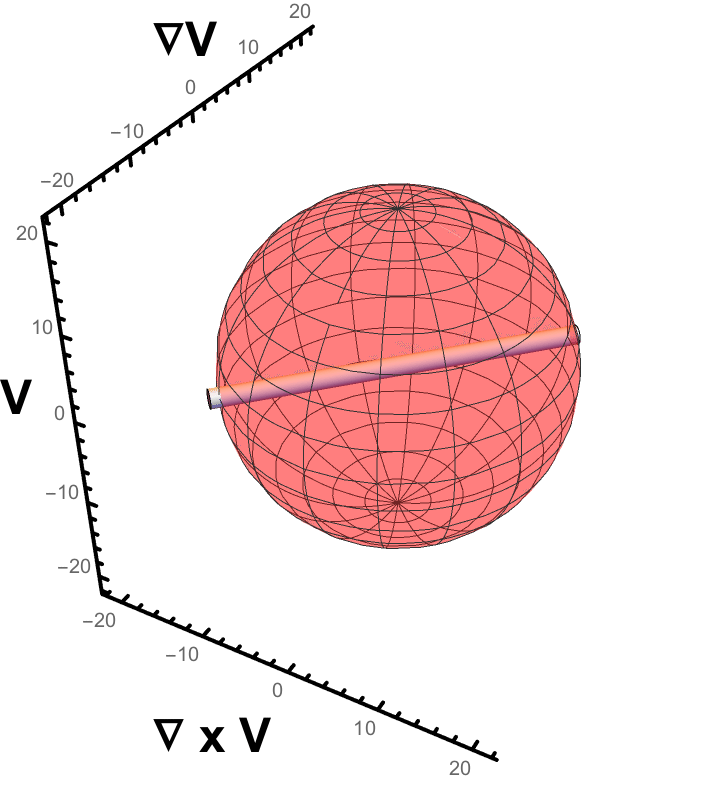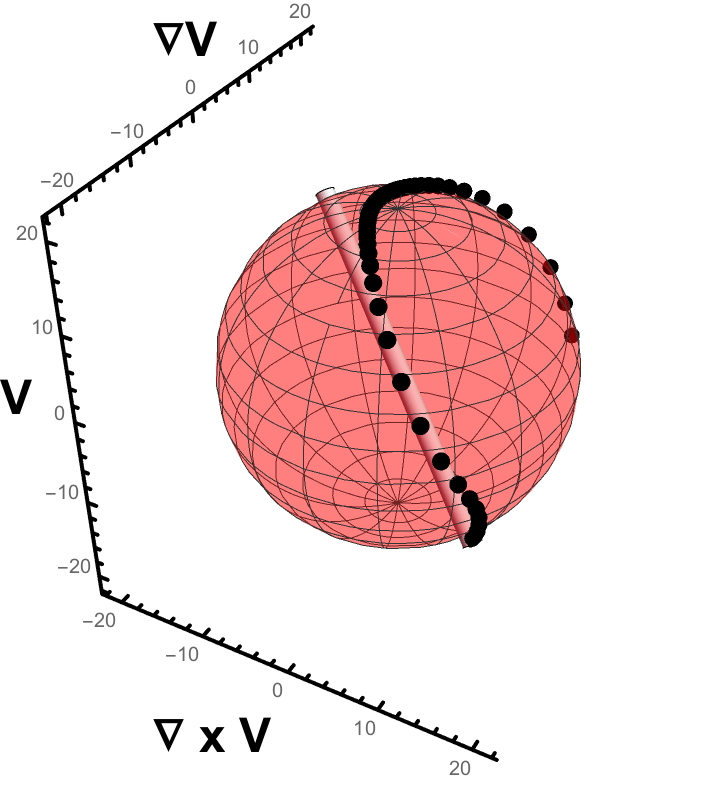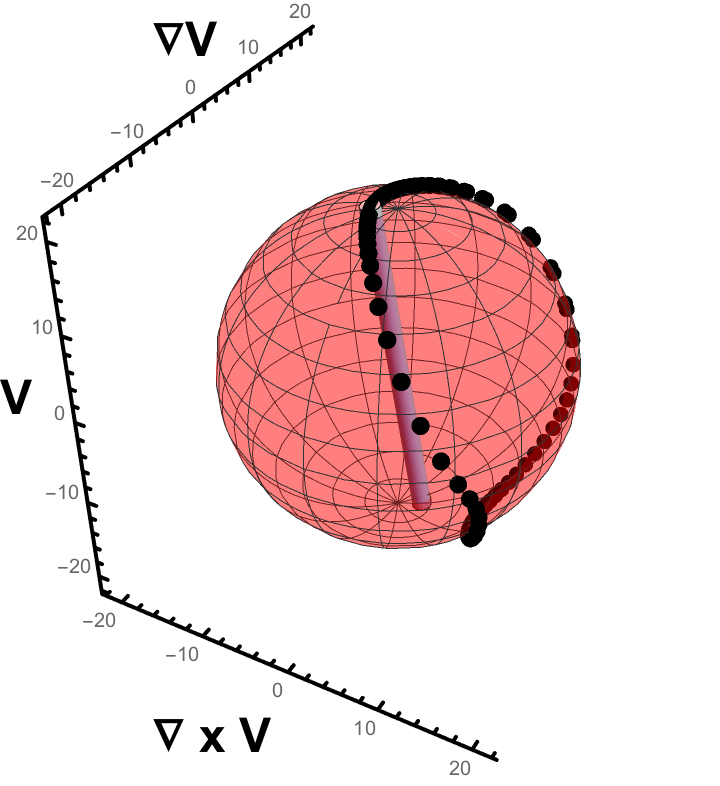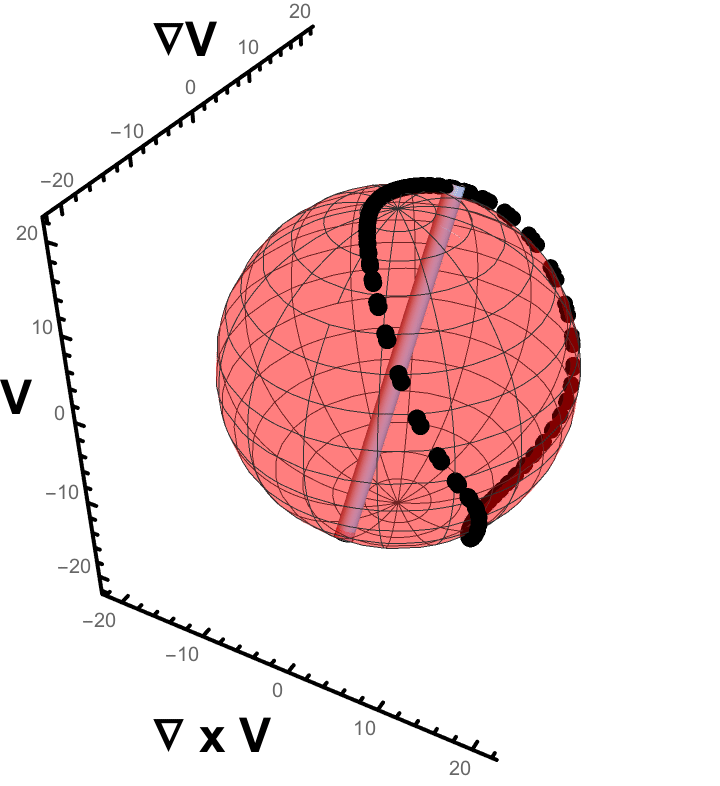
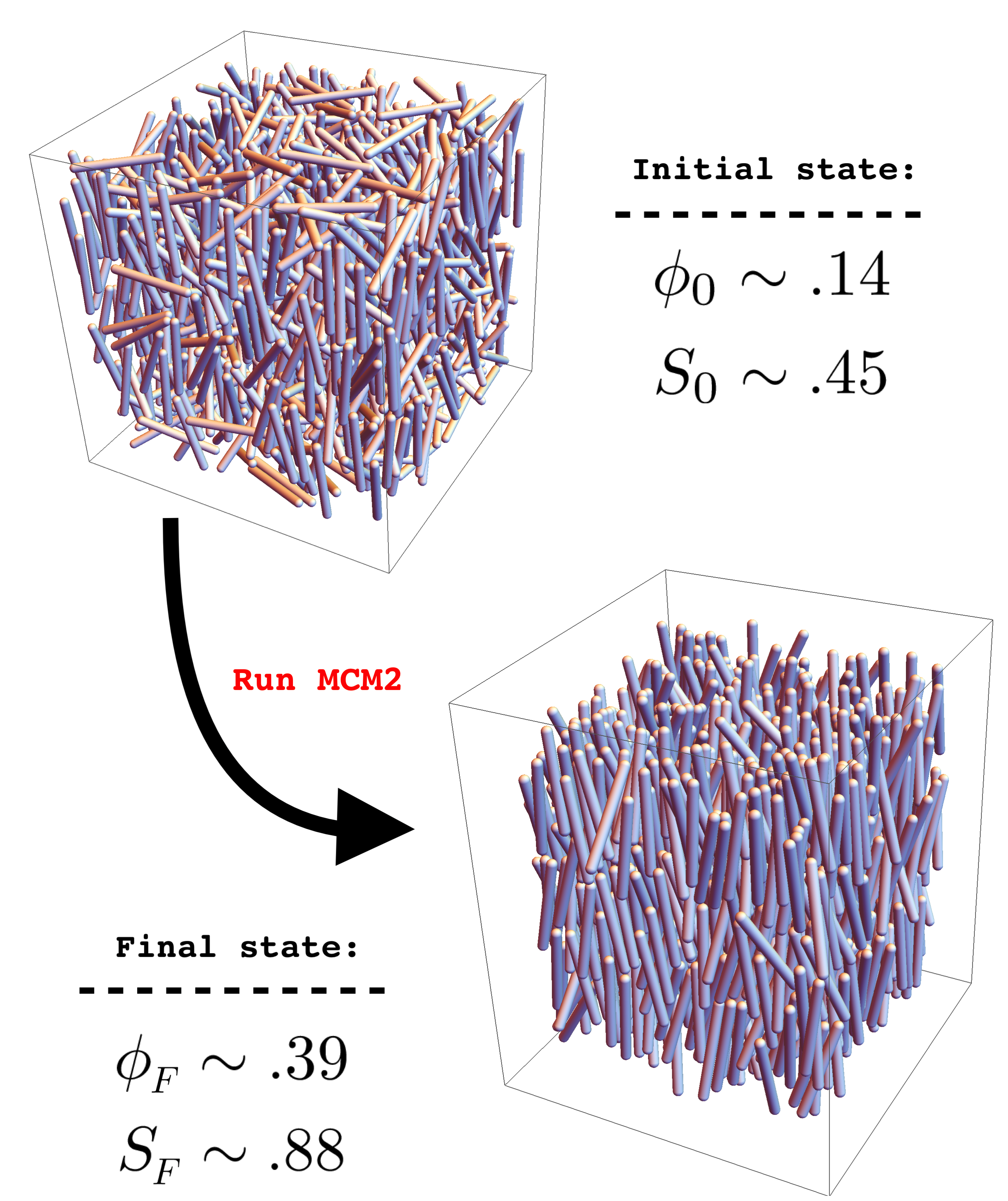
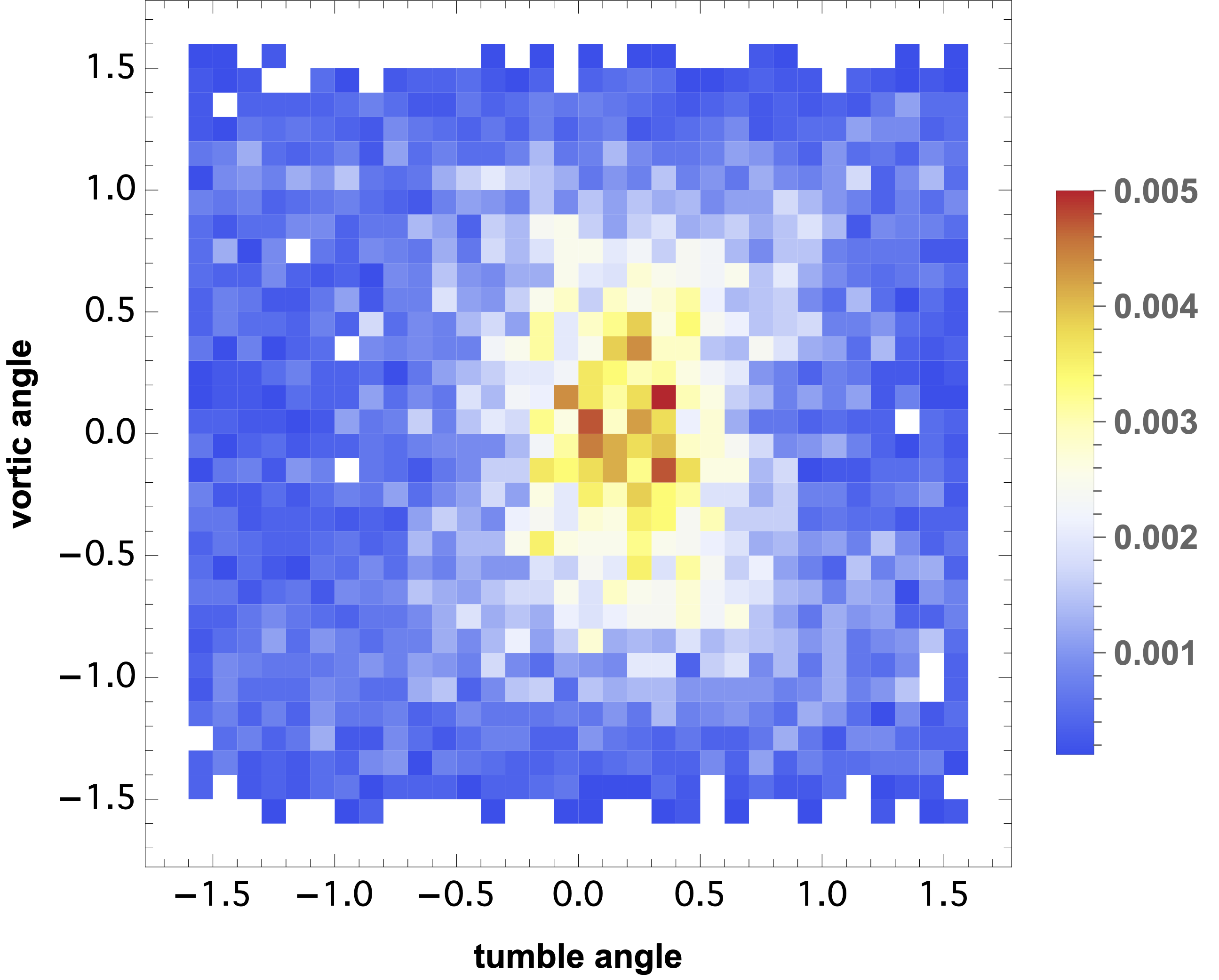
1. This gif shows a single rigid rod under going whats known as a "Jeffery Orbit". (link) Jeffery found that a ellipsoidal particle in a Newtonian fluid under shear will (for low Reynolds number) follow a periodic orbit determined by its aspect ratio. Larger aspect ratio rods tend to point in the flow direction longer (here, this is labelled "v"). These orbits can persist somewhat in the dilute or semi-dilute volume fraction regime, but dont capture the motions of rods in dense suspensions. 2. This image shows the result of the "Mechanical Contraction Method" (link). This is an aglorithm designed to take an initial set of positions and orientations of rigid rods, and then by increasing the volume of the particles slowly, create denser and denser configurations of these rods, all while maintaining that they do not overlap. Here, the initial configuration has a nematic order of roughly .45 and a volume fraction of .14. The end result has an order of .88 and a volume fraction of .39, which is well into the liquid crystal phase. Such dense configurations are crucial to running simulations of frictional liquid crystals. These cannot be formed via methods that attempt to lay down particles randomly one by one, as overlaps arise nearly immediately! 3. The histogram on the left shows the distribution of the orientations of rods under shear, taken from molecular dynamics run in LAMMPS. The data are averaged over 5 strain in steady state, and include the orientations of all 8000 rods. The vertical axis is the angle a given rod takes with respect to the vorticity axis and the flow axis (see the "∇ x v" axis and "v" axis, respectively, in the Jeffery gif). The horizontal is between the gradient axis and flow axis ("∇ v" and "v", respectively).